10 Ejercicios resueltos: Ecuaciones cuadráticas con la fórmula general – Nivel Fácil

Escrito por Diego

Publicado el 11 de Octubre de 2022

10 ejercicios resueltos paso a paso sobre ecuaciones cuadráticas aplicando la fórmula general en nivel fácil.

Te invito a ver esta clase donde se explica la fórmula general y los pasos para aplicarla en ecuaciones cuadráticas, para que puedas resolver estos ejercicios en nivel fácil.

Tabla de contenidos

Ejercicio 1

$x^{2} - x - 6 = 0$

Ver procedimiento y respuesta

Desarrollo:

Identificar los coeficientes a,b y c.

$a = 1$ , $b = -1$ y $c = -6$

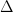Calcular el discriminante ( $\Delta$ ).

$\Delta = b^{2} - 4ac$

$\Delta = (-1)^{2} - 4 \cdot (1) \cdot (-6)$

$\Delta = 1 - (-24)$

$\Delta = 1 + 24$

$\Delta = 25$

$\therefore$ la ecuación tiene dos soluciones reales diferentes.

Aplicar la fórmula general.

$x_{1} = \frac{-b + \sqrt{\Delta }}{2a}$

$x_{1} = \frac{-(-1) + \sqrt{25}}{2 \cdot 1}$

$x_{1} = \frac{1 + 5}{2}$

$x_{1} = \frac{6}{2}$

$x_{1} = 3$

$x_{2} = \frac{-b - \sqrt{\Delta }}{2a}$

$x_{2} = \frac{-(-1) - \sqrt{25}}{2 \cdot 1}$

$x_{2} = \frac{1 - 5}{2}$

$x_{2} = \frac{-4}{2}$

$x_{2} = -2$

Respuesta:

$\boxed{x_{1} = 3}$ y $\boxed{x_{2} = -2}$

Ejercicio 2

$x^{2} + x - 2 = 0$

Ver procedimiento y respuesta

Desarrollo:

Identificar los coeficientes a,b y c.

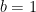$a = 1$ , $b = 1$ y $c = -2$

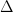Calcular el discriminante ( $\Delta$ ).

$\Delta = b^{2} - 4ac$

$\Delta = (1)^{2} - 4 \cdot (1) \cdot (-2)$

$\Delta = 1 - (-8)$

$\Delta = 1 + 8$

$\Delta = 9$

$\therefore$ la ecuación tiene dos soluciones reales diferentes.

Aplicar la fórmula general.

$x_{1} = \frac{-b + \sqrt{\Delta }}{2a}$

$x_{1} = \frac{-1 + \sqrt{9}}{2 \cdot 1}$

$x_{1} = \frac{-1 + 3}{2}$

$x_{1} = \frac{2}{2}$

$x_{1} = 1$

$x_{2} = \frac{-b - \sqrt{\Delta }}{2a}$

$x_{2} = \frac{-1 - \sqrt{9}}{2 \cdot 1}$

$x_{2} = \frac{-1 - 3}{2}$

$x_{2} = \frac{- 4}{2}$

$x_{2} = -2$

Respuesta:

$\boxed{x_{1} = 1}$ y $\boxed{x_{2} = -2}$

Ejercicio 3

$x^{2} - 5x + 6 = 0$

Ver procedimiento y respuesta

Desarrollo:

Identificar los coeficientes a,b y c.

$a = 1$ , $b = -5$ y $c = 6$

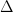Calcular el discriminante ( $\Delta$ ).

$\Delta = b^{2} - 4ac$

$\Delta = (-5)^{2} - 4 \cdot (1) \cdot (6)$

$\Delta = 25 - 24$

$\Delta = 1$

$\therefore$ la ecuación tiene dos soluciones reales diferentes.

Aplicar la fórmula general.

$x_{1} = \frac{-b + \sqrt{\Delta }}{2a}$

$x_{1} = \frac{-(-5) + \sqrt{1}}{2 \cdot 1}$

$x_{1} = \frac{5 + 1}{2}$

$x_{1} = \frac{6}{2}$

$x_{1} = 3$

$x_{2} = \frac{-b - \sqrt{\Delta }}{2a}$

$x_{2} = \frac{-(-5) - \sqrt{1}}{2 \cdot 1}$

$x_{2} = \frac{5 - 1}{2}$

$x_{2} = \frac{4}{2}$

$x_{2} = 2$

Respuesta:

$\boxed{x_{1} = 3}$ y $\boxed{x_{2} = 2}$

Ejercicio 4

$x^{2} - x - 30 = 0$

Ver procedimiento y respuesta

Desarrollo:

Identificar los coeficientes a,b y c.

$a = 1$ , $b = -1$ y $c = -30$

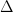Calcular el discriminante ( $\Delta$ ).

$\Delta = b^{2} - 4ac$

$\Delta = (-1)^{2} - 4 \cdot (1) \cdot (-30)$

$\Delta = 1 - (-120)$

$\Delta = 1 + 120$

$\Delta = 121$

$\therefore$ la ecuación tiene dos soluciones reales diferentes.

Aplicar la fórmula general.

$x_{1} = \frac{-b + \sqrt{\Delta }}{2a}$

$x_{1} = \frac{-(-1) + \sqrt{121}}{2 \cdot 1}$

$x_{1} = \frac{1 + 11}{2}$

$x_{1} = \frac{12}{2}$

$x_{1} = 6$

$x_{2} = \frac{-b - \sqrt{\Delta }}{2a}$

$x_{2} = \frac{-(-1) - \sqrt{121}}{2 \cdot 1}$

$x_{2} = \frac{1 - 11}{2}$

$x_{2} = \frac{-10}{2}$

$x_{2} = -5$

Respuesta:

$\boxed{x_{1} = 6}$ y $\boxed{x_{2} = -5}$

Ejercicio 5

$x^{2} +12x + 36 = 0$

Ver procedimiento y respuesta

Desarrollo:

Identificar los coeficientes a,b y c.

$a = 1$ , $b = 12$ y $c = 36$

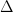Calcular el discriminante ( $\Delta$ ).

$\Delta = b^{2} - 4ac$

$\Delta = (12)^{2} - 4 \cdot (1) \cdot (36)$

$\Delta = 144 - 144$

$\Delta = 0$

$\therefore$ la ecuación tiene dos soluciones reales iguales.

Aplicar la fórmula general.

$x = \frac{-b}{2a}$

$x = \frac{-12}{2 \cdot 1}$

$x = \frac{-12}{2}$

$x = -6$

Respuesta:

$\boxed{x = -6}$

Ejercicio 6

$x^{2} - 3x = 0$

Ver procedimiento y respuesta

Desarrollo:

Identificar los coeficientes a,b y c.

$a = 1$ , $b = -3$ y $c = 0$

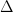Calcular el discriminante ( $\Delta$ ).

$\Delta = b^{2} - 4ac$

$\Delta = (-3)^{2} - 4 \cdot (1) \cdot (0)$

$\Delta = 9 - 0$

$\Delta = 9$

$\therefore$ la ecuación tiene dos soluciones reales diferentes.

Aplicar la fórmula general.

$x_{1} = \frac{-b + \sqrt{\Delta }}{2a}$

$x_{1} = \frac{-(-3) + \sqrt{9}}{2 \cdot 1}$

$x_{1} = \frac{3 + 3}{2}$

$x_{1} = \frac{6}{2}$

$x_{1} = 3$

$x_{2} = \frac{-b - \sqrt{\Delta }}{2a}$

$x_{2} = \frac{-(-3) - \sqrt{9}}{2 \cdot 1}$

$x_{2} = \frac{3 - 3}{2}$

$x_{2} = \frac{0}{2}$

$x_{2} = 0$

Respuesta:

$\boxed{x_{1} = 3}$ y $\boxed{x_{2} = 0}$

Ejercicio 7

$x^{2} - 25 = 0$

Ver procedimiento y respuesta

Desarrollo:

Identificar los coeficientes a,b y c.

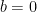$a = 1$ , $b = 0$ y $c = -25$

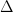Calcular el discriminante ( $\Delta$ ).

$\Delta = b^{2} - 4ac$

$\Delta = 0^{2} - 4 \cdot (1) \cdot (-25)$

$\Delta = 0 - (-100)$

$\Delta = 0 + 100$

$\Delta = 100$

$\therefore$ la ecuación tiene dos soluciones reales diferentes.

Aplicar la fórmula general.

$x_{1} = \frac{-b + \sqrt{\Delta }}{2a}$

$x_{1} = \frac{-0 + \sqrt{100}}{2 \cdot 1}$

$x_{1} = \frac{-0 +10}{2}$

$x_{1} = \frac{10}{2}$

$x_{1} = 5$

$x_{2} = \frac{-b - \sqrt{\Delta }}{2a}$

$x_{2} = \frac{-0 - \sqrt{100}}{2 \cdot 1}$

$x_{2} = \frac{-0 - 10}{2}$

$x_{2} = \frac{-10}{2}$

$x_{2} = -5$

Respuesta:

$\boxed{x_{1} = 5}$ y $\boxed{x_{2} = -5}$

Ejercicio 8

$x^{2} + 5x - 36 = 0$

Ver procedimiento y respuesta

Desarrollo:

Identificar los coeficientes a,b y c.

$a = 1$ , $b = 5$ y $c = -36$

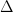Calcular el discriminante ( $\Delta$ ).

$\Delta = b^{2} - 4ac$

$\Delta = (5)^{2} - 4 \cdot (1) \cdot (-36)$

$\Delta = 25 - (-144)$

$\Delta = 25 + 144$

$\Delta = 169$

$\therefore$ la ecuación tiene dos soluciones reales diferentes.

Aplicar la fórmula general.

$x_{1} = \frac{-b + \sqrt{\Delta }}{2a}$

$x_{1} = \frac{-5 + \sqrt{169}}{2 \cdot 1}$

$x_{1} = \frac{-5 + 13}{2}$

$x_{1} = \frac{8}{2}$

$x_{1} = 4$

$x_{2} = \frac{-b - \sqrt{\Delta }}{2a}$

$x_{2} = \frac{-5 - \sqrt{169}}{2 \cdot 1}$

$x_{2} = \frac{-5 - 13}{2}$

$x_{2} = \frac{-18}{2}$

$x_{2} = -9$

Respuesta:

$\boxed{x_{1} = 4}$ y $\boxed{x_{2} = -9}$

Ejercicio 9

$x^{2} + 7x = 0$

Ver procedimiento y respuesta

Desarrollo:

Identificar los coeficientes a,b y c.

$a = 1$ , $b = 7$ y $c = 0$

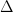Calcular el discriminante ( $\Delta$ ).

$\Delta = b^{2} - 4ac$

$\Delta = (7)^{2} - 4 \cdot (1) \cdot (0)$

$\Delta = 49 - 0$

$\Delta = 49$

$\therefore$ la ecuación tiene dos soluciones reales diferentes.

Aplicar la fórmula general.

$x_{1} = \frac{-b + \sqrt{\Delta }}{2a}$

$x_{1} = \frac{-7 + \sqrt{49}}{2 \cdot 1}$

$x_{1} = \frac{-7 + 7}{2}$

$x_{1} = \frac{0}{2}$

$x_{1} = 0$

$x_{2} = \frac{-b - \sqrt{\Delta }}{2a}$

$x_{2} = \frac{-7 - \sqrt{49}}{2 \cdot 1}$

$x_{2} = \frac{-7 - 7}{2}$

$x_{2} = \frac{-14}{2}$

$x_{2} = -7$

Respuesta:

$\boxed{x_{1} = 0}$ y $\boxed{x_{2} = -7}$

Ejercicio 10

$x^{2} - 2x + 1 = 0$

Ver procedimiento y respuesta

Desarrollo:

Identificar los coeficientes a,b y c.

$a = 1$ , $b = -2$ y $c = 1$

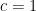
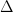Calcular el discriminante ( $\Delta$ ).

$\Delta = b^{2} - 4ac$

$\Delta = (-2)^{2} - 4 \cdot (1) \cdot (1)$

$\Delta = 4 - 4$

$\Delta = 0$

$\therefore$ la ecuación tiene dos soluciones reales iguales.

Aplicar la fórmula general.

$x = \frac{-b}{2a}$

$x = \frac{-(-2)}{2 \cdot 1}$

$x = \frac{2}{2}$

$x = 1$

Respuesta:

$\boxed{x = 1}$

Aquí terminan los 10 Ejercicios resueltos sobre resolver ecuaciones cuadráticas utilizando la fórmula general en nivel fácil. Recuerda seguirnos en Instagram.